Shannon entropy

When it comes down to it, files are just a sequence of bytes. So how do you go about measuring how random a file is?

Quick solution

A quick and dirty solution is to just sum the number of times each byte appears. In more "random" files the totals for each byte should be similar. In less "random" files the totals will be further apart.

xxd can be used to represent each byte in a file has hex:

$ xxd --cols 1 input.dat
00000000: 48  H
00000001: 65  e
00000002: 6c  l
00000003: 6c  l
00000004: 6f  o
00000005: 20
00000006: 77  w
00000007: 6f  o
00000008: 72  r
00000009: 6c  l
0000000a: 64  d
0000000b: 0a  .

sort, uniq and awk can then be used to count how frequently each byte occurs:

$ xxd --cols 1 input.dat | awk '{print $2}' | sort | uniq -c
      1 0a
      1 20
      1 48
      1 64
      1 65
      3 6c
      2 6f
      1 72
      1 77

There are, however 2⁸ distinct bytes. One way to simplify this is to total the hex characters instead of the actual bytes. This can be done by modifying the awk program slightly:

xxd --cols 1 input.dat | awk '{split($2, a, ""); print a[1]; print a[2]}' | sort | uniq -c

Running this against a random file should normally show an even distribution:

$ dd if=/dev/urandom of=input.dat bs=1024 count=10
10+0 records in
10+0 records out
10240 bytes (10 kB) copied, 0.00942794 s, 1.1 MB/s
$ xxd --cols 1 input.dat | awk '{split($2, a, ""); print a[1]; print a[2]}' | sort | uniq -c
   1243 0
   1342 1
   1305 2
   1254 3
   1283 4
   1206 5
   1353 6
   1257 7
   1331 8
   1317 9
   1244 a
   1254 b
   1301 c
   1273 d
   1275 e
   1242 f

However, data such as plain text produces a more uneven distribution:

$ cat /usr/share/doc/*/README > input.dat
$ xxd --cols 1 input.dat | awk '{split($2, a, ""); print a[1]; print a[2]}' | sort | uniq - c
 237356 0
  56694 1
 307517 2
 103665 3
 138791 4
 138875 5
 494074 6
 259974 7
  35107 8
  77824 9
  35590 a
   7286 b
  42315 c
  39018 d
  65413 e
  65121 f

A more formal approach

A more formal way to look at how "random" a file is, is to calculate its entropy. In information theory, entropy is a measure of unpredictability in information content. Shannon entropy can be calculated with the following formula:

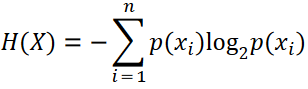
Implementing the equation above involves the following steps:

1. Count the number of times each byte appears in a file.
2. Calculate the probability, p(x), for each byte. This will be the number of times the byte appears in the file, divided by the number of bytes in the file.
3. Multiply each probability, by the base two logarithm of the probability.
4. Finally total the results from the previous step, and take the absolute value. This will give the average entropy per byte, H(X).

The steps above can easily be implemented in a few lines of Python. If you're interested in learning more about information theory, Claude Shannon's paper, A Mathematical Theory of Communication, discusses entropy in far greater detail. If you haven't already guessed, Shannon entropy is named after Claude Shannon.

Encryption, compression and entropy

So why is calculating entropy useful? Well, it makes it very easy to distinguish plain text from Ciphertext. Plain text will have relatively low entropy per byte:

$ cat /usr/share/doc/*/README | ./shannon_entropy.py
bytes        : 1052310
entropy      : 5145048
entropy/byte : 4.889290

Encrypting the text will significantly increase the entropy per byte:

$ cat /usr/share/doc/*/README | gpg2 --batch --passphrase secret_key --symmetric -o - - | ./ shannon_entropy.py
bytes        : 392180
entropy      : 3137215
entropy/byte : 7.999428

It is however worth noting that encrypted files, are not the only sort of file with high entropy per byte. Lossless compression tools like gzip will reduce repeating patterns, thereby increasing entropy per byte:

$ cat /usr/share/doc/*/README | gzip | ./shannon_entropy.py
bytes        : 355186
entropy      : 2840820
entropy/byte : 7.998122

Files compressed with lossy compression, such as JPEG, will also have high entropy per byte values:

$ ./shannon_entropy.py picture.jpg
bytes        : 27958
entropy      : 222870
entropy/byte : 7.971627